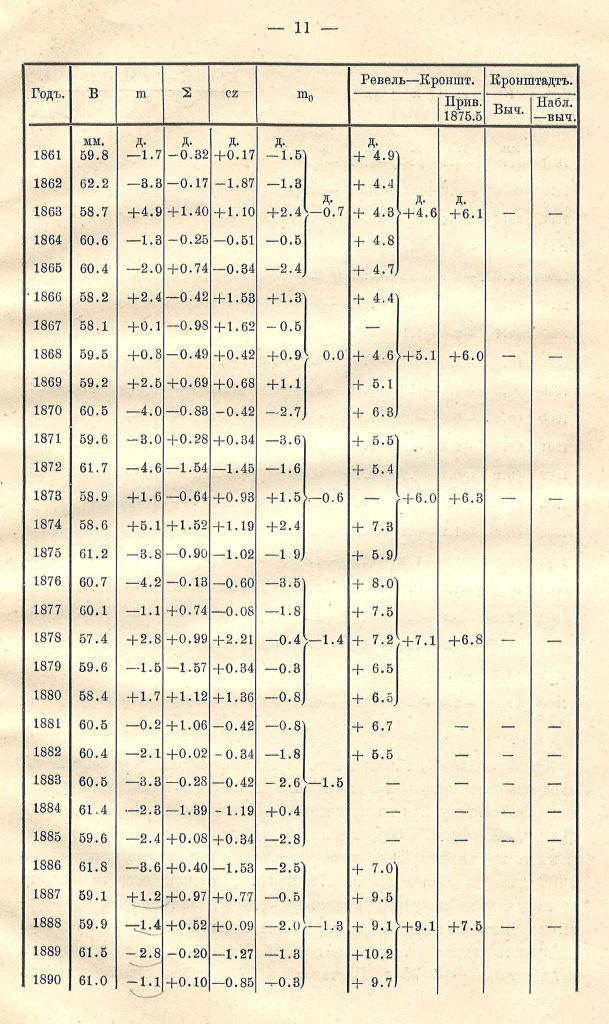
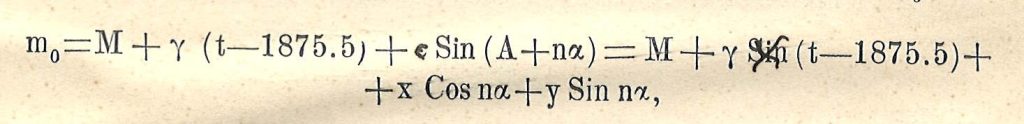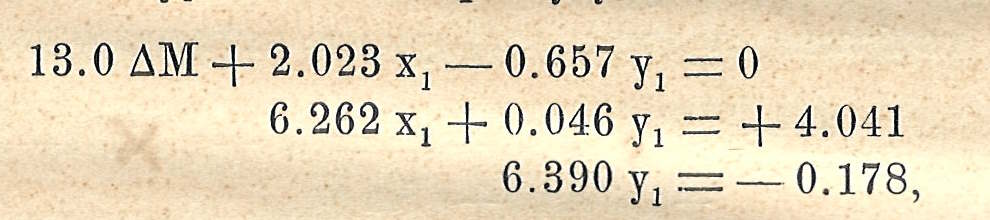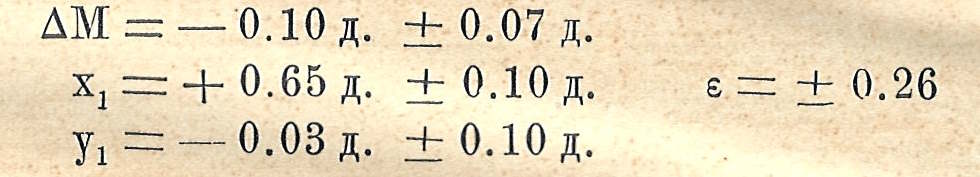Средний уровень моря у Кронштадта.
по наблюдениям 1841—1910 г.г. продолжение.
—11—
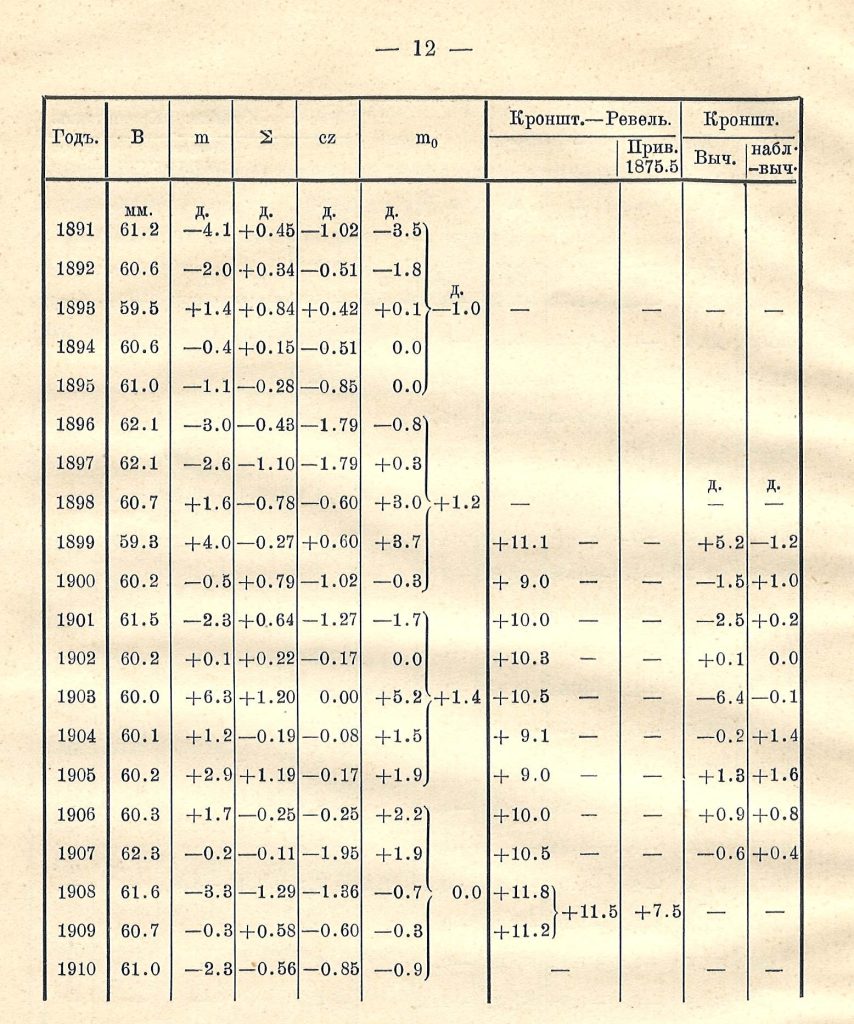
—12—
Относительно наблюденных средних годовых уровней m, следует заметить, что в начале 1909 года было обнаружено несогласие между нулем футштока и основною маркою, по определению X. Фр. Тонберга, на 1.0 дюйм, на который нуль оказался ниже марки. Так как футшток был поставлен в мае 1908 года, а снят в мае 1909 года, то все отсчеты за это время должны получить поправку — 1.0 д.; заменивший его футшток был поставлен на 13/4 дюйма выше и стоял до 1 октября (Сборник гидро-метеор, наблюдений, вып. IX); его поправка следовательно +0.75 д. Поставленный 1 октября новый футшток
—13—
был согласован с маркою и до 1 мая 1910 г. имел, поэтому, поправку нуль. Наконец от мая по декабрь 1910 г., по определенно г-на Тонберга, наблюдения должны получить поправку +0.5 д. В сопоставлении показаны годовые уровни уже исправленные этими поправками и, потому, они могут считаться верными.
Замеченное в 1908 году несогласие между нулем футштока и маркою, вызывает недоверие к наблюдениям целого ряда предшествующих лет, начиная с 1894 г. Для того, чтобы, может быть, получить некоторое указание о величине подозреваемых ошибок, я прибег к наблюдениям над уровнем моря в Ревеле, где производились наблюдения с 1842 года, сначала, до 1873 года, по футштоку, установленному М. Ф. Рейнеке, одновременно с футштоком в Кронштадте; позже наблюдения делались на других футштоках, связь которых с первым, однако, удалось установить. Все данные для приведения наблюдений к нулю футштока Рейнеке, находятся в сочинении С. Д. Рыльке «Средний уровень Балтийского, Черного и Азовского морей. 1895». Взятые оттуда годовые средние уровни для Ревеля, не исправленные ни за влияние ветра, ни за давление атмосферы, я сравнил с такими же средними для Кронштадта, т. е. с величинами m данного выше сопоставления. Полученные разности для всех годов, для которых имеются данные у Рыльке, а для последнего времени в «Сборнике гидро-метеор, набл. (с 1899 г.)», приведены в сопоставлении в столбце Рев.—Кронш. Как видно, ряды смежных годов, за немногими исключениями, показывают хорошее соглашение между собой и обнаруживается с большою явственностью, в особенности в средних величинах, постепенное увеличение разности.
Если приписать отклонениям уровней смежных годов от их среднего, характер случайных ошибок, то для вероятной погрешности годовой разности Рев.—Кронш. получается +0.56 д., а для пятилетнего среднего +0.25 д. Для вывода вероятной величины постепенного изменения разности были употреблены пяти или четырех—летние средние (последнее из средних составлено по двум только годам 1908—9), за исключением тех, которые подлежат сомнению, т. е. 1899—1907 г. г.
Решение 10 уравнений по способу наименьших квадратов дает:
разн. Рев.—Кронш.=Δm= + 7.05 д.+0.120 д. (t—1875.5)
±0.71 +0.24 +0.012
—14—
Рыльке, в названном своем сочинении, вывел годовое изменение уровня у Ревеля ±0.130 д. ±0.027, что, как видно, близко согласуется с выведенным здесь изменением разности Рев.—Кронш.; следовательно можно заключить, что годовое изменение в Кронштадте может быть только очень небольшое.
При помощи найденного годового изменения все пятилетние средние разности приведены к средней эпохе 1875.5; таким образом приведенные величины, в сопоставлении показаны рядом с наблюденными. Нельзя не считать согласие между величинами, приведенными к одной эпохе, весьма хорошим, хотя очевидно, что в них осталось еще некоторое периодическое изменение; подобное же изменение, как увидим дальше, обнаруживается в уровнях Кронштадтских; первое, поэтому есть следствие второго.
Пользуясь выражением для Δm и с наблюденными в Ревеле средними годовыми уровнями за время 1899—1907 г., выведены были уровни, которые, судя по Ревелю, должны были быть в Кронштадте в названные годы; они показаны в последнем столбце, вместе с отклонением их от действительно наблюденных в Кронштадте уровнен т. е. m.
Судя по этим отклонениям, наблюдения, которые мы предположили сомнительными, ни в отношении внутреннего согласия, ни в отношении какой-нибудь постоянной погрешности, не хуже других. В виду этого едва ли возможно пренебрегать ими вовсе; но, чтобы не оставить без всякого внимания то обстоятельство, что в 1908 году была обнаружена ошибка в установке футштока, можно придать меньший вес всем наблюдениям 1894—1907 г. г. В последующему при выводе среднего уровня и его годового изменения по пятилетним средним, я придал вес 1/2 двум предпоследним средним и тоже двум годовым средним 1906 и 1907, при выводе последнего из пятилетних средних.
Если составить для величин пятилетних средних m0 условный уравнения вида
и решить эти уравнения по способу наименьших квадратов, относительно веса поступая по сейчас сказанному, то получается:
—15—
Если сравнить величины отдельных годов с соответствующими пятилетними средними, то по отклонениям получаемая вероятная погрешность одного такого пятилетнего среднего, получается ±0.59, т. е. приблизительно такая же, какая получается при решении уравнений. Судя поэтому, принятое выражение для m0 вполне удовлетворяет наблюдениям. Но рассматривая отклонения, остающиеся после вставления найденных вероятных величин двух неизвестных М и ϒ в условные уравнения, отклонения, который показаны в следующей дальше табличке в столбце Გ1, нельзя не заметить некоторую, проявляющуюся в них периодичность: высказываются в них три максимума и два минимума, причем период приблизительно тридцатилетний; при этом, однако, средний максимум несколько меньше других, так что для объяснения отклонений одного периода, очевидно, недостаточно. В виде приближения я принял пока один только тридцатилетний период и, сообразно с этим, следующее выражение для m0:
где na есть кратное угла 60° (при пятилетних средних); начало счета пусть совпадает с 1843.5 годом; для краткости положено х = с Sin А и у = с Cos А.
Решение 14 условных уравнений с четырьмя неизвестными приводить к следующим нормальным уравнениям, придерживаясь относительно веса к сказанному выше:
Величинам х и у соответствует А = + 129°75 и С = 0°92 д., а это значить, что mах. величины m0 случается при а = 320°25, или в 1840.2, 1870.2 и т. д. годах, a min. при а = 140°25, или 1855.2, 1885.2 и т. д. годах.
—16—
Как видно вер. погр. уравнения веса 1, здесь получается несколько меньше, чем при первом приближении с двумя только неизвестными; но и теперь еще в отклонениях Გ2, остающихся после вставления вероятных величин неизвестных в условные уравнения, заметна периодичность, как это можно было предвидеть: около 1853 и 1903 гг. заметен максимум, а по середине между ними — минимум, т. е. проявляется период приблизительно в 50 лет. Поэтому, в виде 3-2 приближения, были составлены условный уравнения следующего вида:
где Გ2 суть остающиеся отклонения при втором приближении, ΔМ поправка полученного там среднего уровня М, nβ кратное угла 36°, а х = σ Sin β и у = σ Cos β; для начала счета угла β принять год 1853.5.
Нормальные уравнения теперь будут:
откуда:
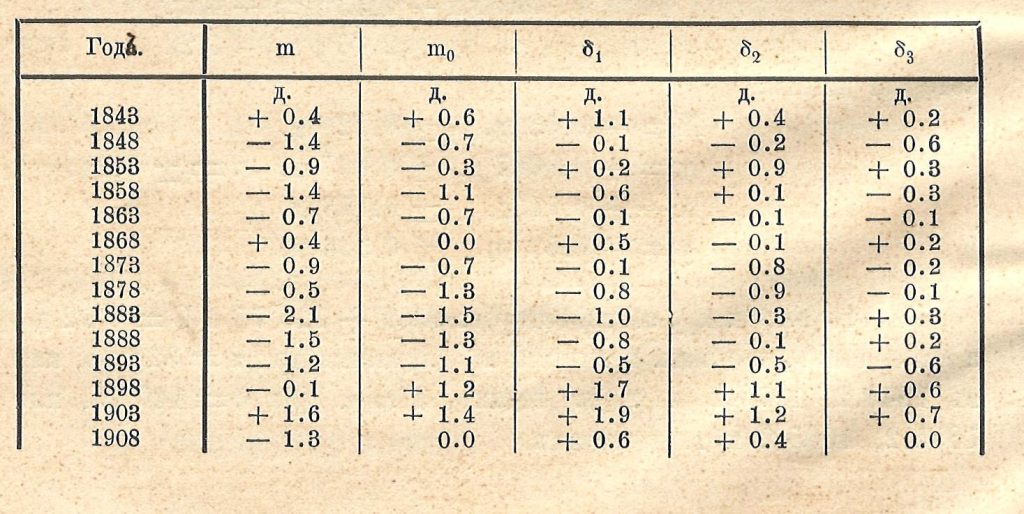
Найденным величинам х1 и у1: соответствуют В = 92°9 и d = 0.65 д. При последнем решении величина ɛ, т. е. вер. погр. уравнения с весом 1, получилась значительно меньше, чем раньше и остающиеся отклонения Გ3 весьма невелики. В следующей табличке сопоставлены величины m1 и m0 и остающаяся при трех приближениях отклонения Გ1,Გ2 и Გ3
Если периодичность в величинах m0, в роде найденной, действительно существует и полученная величина для ɛ имеет реальное значение, то обстоятельство, что она значительно меньше той вероятной погрешности ±0.59 д., которая получается для одного пятилетнего среднего по отклонениям отдельных лет от соответствующего пятилетнего среднего, приписывая этим отклонениям характер случайных ошибок, указывало бы на то, что изменения уровня из года в год не имеют характера случайных ошибок, а что в ряде лет происходит компенсация в большей мере, чем она происходить при случайных изменениях.
Хотя, по предыдущему, введение периодичности колебаний уровня заметно уменьшает отклонения вычисленных уровней от наблюденных, считать доказанным существование подобных периодов по имеемым данным, едва ли возможно, так как амплитуды колебаний слишком мало превышают величину остающихся отклонений и продолжительность наблюдений еще слишком мала; решит вопрос могут только наблюдения последующих лет. Для 30-ти летнего периода можно бы еще найти объяснение в период Брюкнера, но для периода 50-ти летнего, на сколько мне известно, не имеется оснований.
Главный, занимающий нас вопрос о среднем уровне моря и о вековом его изменении, почти совсем не затрагивается неопределенностью относительно периодичности колебаний: средний уровень М при всех трех решениях получается почти один и тот же, в пределах вероятных ошибок; что касается векового изменения уровня, то оно, по совокупности наблюдений, ничтожно и за 100 лет не выходить из пределов дюйма.
Таким образом, по наблюдениям 1841—1910 гг. получается, что в Кронштадте средний уровень моря ниже марки на 0,5 дюйма + 0.15 д.
Этот средний уровень соответствует средним направлению и силе ветра, а также и среднему давлению атмосферы.
В. Фус.
Отдельные оттиски из Записок по Гидрографии. 1911 г. Вып. XXXIII.
Типография Морского Министерства, в Главном Адмиралтействе.
Навигация: Страница 1 2